What are the most mindblowing things in mathematics?

What concepts or facts do you know from math that is mind blowing, awesome, or simply fascinating?
Here are some I would like to share:
- Gödel's incompleteness theorems: There are some problems in math so difficult that it can never be solved no matter how much time you put into it.
- Halting problem: It is impossible to write a program that can figure out whether or not any input program loops forever or finishes running. (Undecidablity)
The Busy Beaver function
Now this is the mind blowing one. What is the largest non-infinite number you know? Graham's Number? TREE(3)? TREE(TREE(3))? This one will beat it easily.
- The Busy Beaver function produces the fastest growing number that is theoretically possible. These numbers are so large we don't even know if you can compute the function to get the value even with an infinitely powerful PC.
- In fact, just the mere act of being able to compute the value would mean solving the hardest problems in mathematics.
- Σ(1) = 1
- Σ(4) = 13
- Σ(6) > 10^10^10^10^10^10^10^10^10^10^10^10^10^10^10 (10s are stacked on each other)
- Σ(17) > Graham's Number
- Σ(27) If you can compute this function the Goldbach conjecture is false.
- Σ(744) If you can compute this function the Riemann hypothesis is false.
Sources:
- YouTube - The Busy Beaver function by Mutual Information
- YouTube - Gödel's incompleteness Theorem by Veritasium
- YouTube - Halting Problem by Computerphile
- YouTube - Graham's Number by Numberphile
- YouTube - TREE(3) by Numberphile
- Wikipedia - Gödel's incompleteness theorems
- Wikipedia - Halting Problem
- Wikipedia - Busy Beaver
- Wikipedia - Riemann hypothesis
- Wikipedia - Goldbach's conjecture
- Wikipedia - Millennium Prize Problems - $1,000,000 Reward for a solution
There are more ways to arrange a deck of 52 cards than there are atoms on Earth.
52 Factorial
I feel this one is quite well known, but it's still pretty cool.
An extension of that is that every time you shuffle a deck of cards there's a high probability that that particular arrangement has never been seen in the history of mankind.
With the caveat that it's not the first shuffle of a new deck. Since card decks come out of the factory in the same order, the probability that the first shuffle will result in an order that has been seen before is a little higher than on a deck that has already been shuffled.
Since a deck of cards can only be shuffled a finite number of times before they get all fucked up, the probability of deck arrangements is probably a long tail distribution
The most efficient way is not to shuffle them but to lay them all on a table, shift them around, and stack them again in arbitrary order.
assuming a perfect mechanical shuffle, I think the odds are near zero. humans don't shuffle perfectly though!
What's perfect in this context? It's maybe a little counterintuitive because I'd think a perfect mechanical shuffle would be perfectly deterministic (assuming no mechanical failure of the device) so that it would be repeatable. Like, you would give it a seed number (about 67 digits evidently) and the mechanism would perform a series of interleaves completely determined by the seed. Then if you wanted a random order you would give the machine a true random seed (from your wall of lava lamps or whatever) and you'd get a deck with an order that is very likely to never have been seen before. And if you wanted to play a game with that particular deck order again you'd just put the same seed into the machine.
Perfect is the sense that you have perfect randomness. Like the Fisher-Yates shuffle.
In order to have a machine that can "pick" any possible shuffle by index (that's all a seed really is, a partial index into the space of random numbers), you'd need a seed 223 bits long.
But you wouldn't want perfect mechanical shuffles though because 8 perfect riffles will loop the deck back to it's original order! The minor inaccuracies are what makes actual shuffling work.
I'd probably have the machine do it all electronically and then sort the physical deck to match, not sure you could control the entropy in a reliable way with actual paper cards otherwise.
For the uninitiated, the monty Hall problem is a good one.
Start with 3 closed doors, and an announcer who knows what's behind each. The announcer says that behind 2 of the doors is a goat, and behind the third door is
a carstudent debt relief, but doesn't tell you which door leads to which. They then let you pick a door, and you will get what's behind the door. Before you open it, they open a different door than your choice and reveal a goat. Then the announcer says you are allowed to change your choice.So should you switch?
The answer turns out to be yes. 2/3rds of the time you are better off switching. But even famous mathematicians didn't believe it at first.
I know the problem is easier to visualize if you increase the number of doors. Let's say you start with 1000 doors, you choose one and the announcer opens 998 other doors with goats. In this way is evident you should switch because unless you were incredibly lucky to pick up the initial door with the prize between 1000, the other door will have it.
I now recall there was a numberphile with exactly that visualisation! It's a clever visual
It really is, it's how my probability class finally got me to understand why this solution is true.
This is so mind blowing to me, because I get what you're saying logically, but my gut still tells me it's a 50/50 chance.
But I think the reason it is true is because the other person didn't choose the other 998 doors randomly. So if you chose any of the other 998 doors, it would still be between the door you chose and the winner, other than the 1/1000 chance that you chose right at the beginning.
I don't find this more intuitive. It's still one or the other door.
The point is, the odds don't get recomputed after the other doors are opened. In effect you were offered two choices at the start: choose one door, or choose all of the other 999 doors.
This is the way to think about it.
The thing is, you pick the door totally randomly and since there are more goats, the chance to pick a goat is higher. That means there's a 2/3 chance that the door you initially picked is a goat. The announcer picks the other goat with a 100% chance, which means the last remaining door most likely has the prize behind it
Edit: seems like this was already answered by someone else, but I didn't see their comment due to federation delay. Sorry
Don't be sorry, your comment was the first time I actually understood how it works. Like I understand the numbers, but I still didn't get the problem, even when increasing the amount of doors. It was your explanation that made it actually click.
I think the problem is worded specifically to hide the fact that you're creating two set of doors by picking a door, and that shrinking a set actually make each individual door in that set more likely to have the prize.
Think of it this way : You have 4 doors, 2 blue doors and 2 red doors. I tell you that there is 50% chance of the prize to be in either a blue or a red door. Now I get to remove a red door that is confirmed to not have the prize. If you had to chose, would you pick a blue door or a red door? Seems obvious now that the remaining red door is somehow a safer pick. This is kind of what is happening in the initial problem, but since the second ensemble is bigger to begin with (the two doors you did not pick), it sort of trick you into ignoring the fact that the ensemble shrank and that it made the remaining door more "valuable", since the two ensembles are now of equal size, but only one ensemble shrank, and it was always at 2/3 odds of containing the prize.
The odds you picked the correct door at the start is 1/1000, that means there's a 999/1000 chance it's in one of the other 999 doors. If the man opens 998 doors and leaves one left then that door has 999/1000 chance of having the prize.
Same here, even after reading other explanations I don't see how the odds are anything other than 50/50.
read up on the law of total probability. prob(car is behind door #1) = 1/3. monty opens door #3, shows you a goat. prob(car behind door #1) = 1/3, unchanged from before. prob(car is behind door #2) + prob(car behind door #1) = 1. therefore, prob(car is behind door #2) = 2/3.
Following that cascade, didn't you just change the probability of door 2? It was 1/3 like the other two. Then you opened door three. Why would door two be 2/3 now? Door 2 changes for no disclosed reason, but door 1 doesn't? Why does door 1 have a fixed probability when door 2 doesn't?
No, you didn’t change the prob of #2. Prob(car behind 2) + prob(car behind 3) = 2/3. Monty shows you that prob(car behind 3) = 0.
This can also be understood through conditional probabilities, if that’s easier for you.
How do we even come up with such amazing problems right ? It's fascinating.
This is fantastic, thank you.
They emphatically did not believe it at first. Marilyn vos Savant was flooded with about 10,000 letters after publishing the famous 1990 article, and had to write two followup articles to clarify the logic involved.
Oh that's cool - I had heard one or two examples only. Is there some popular writeup of the story from Savant's view?
I couldn't tell you - I used the Wikipedia article to reference the specifics and I'm not sure where I first heard about the story. I just remember that the mathematics community dogpiled on her hard for some time and has since completely turned around to accept her answer as correct.
Also relevant - she did not invent the problem, but her article is considered by some to have been what popularized it.
I know it to be true, I've heard it dozens of times, but my dumb brain still refuses to accept the solution everytime. It's kind of crazy really
To me, it makes sense because there was initially 2 chances out of 3 for the prize to be in the doors you did not pick. Revealing a door, exclusively on doors you did not pick, does not reset the odds of the whole problem, it is still more likely that the prize is in one of the door you did not pick, and a door was removed from that pool.
Imo, the key element here is that your own door cannot be revealed early, or else changing your choice would not matter, so it is never "tested", and this ultimately make the other door more "vouched" for, statistically, and since you know that the door was more likely to be in the other set to begin with, well, might as well switch!
Let's name the goats Alice and Bob. You pick at random between Alice, Bob, and the Car, each with 1/3 chance. Let's examine each case.
Case 1: You picked Alice. Monty eliminates Bob. Switching wins. (1/3)
Case 2: You picked Bob. Monty eliminates Alice. Switching wins. (1/3)
Case 3: You picked the Car. Monty eliminates either Alice or Bob. You don't know which, but it doesn't matter-- switching loses. (1/3)
It comes down to the fact that Monty always eliminates a goat, which is why there is only one possibility in each of these (equally probable) cases.
From another point of view: Monty revealing a goat does not provide us any new information, because we know in advance that he must always do so. Hence our original odds of picking correctly (p=1/3) cannot change.
In the variant "Monty Fall" problem, where Monty opens a random door, we perform the same analysis:
As you can see, there is now a chance that Monty reveals the car resulting in an instant game over-- a 1/3 chance, to be exact. If Monty just so happens to reveal a goat, we instantly know that cases 1b and 2b are impossible. (In this variant, Monty revealing a goat reveals new information!) Of the remaining (still equally probable!) cases, switching wins half the time.
like on paper the odds on your original door was 1/3 and the option door is 1/2, but in reality with the original information both doors were 1/3 and now with the new information both doors are 1/2.
Your original odds were 1/3, and this never changes since you don't get any new information.
The key is that Monty always reveals a goat. No matter what you choose, even before you make your choice, you know Monty will reveal a goat. Therefore, when he does so, you learn nothing you didn't already know.
Yes, you don't actually have to switch. You could also throw a coin to decide to stay at the current door or to switch. By throwing a coin, you actually improved your chances of winning the price.
This is incorrect. The way the Monty Hall problem is formulated means staying at the current door has 1/3 chance of winning, and switching gives you 2/3 chance. Flipping a coin doesn't change anything. I'm not going to give a long explanation on why this is true since there are plenty other explanations in other comments already.
This is a common misconception that switching is better because it improves your chances from 1/3 to 1/2, whereas it actually increases to 2/3.
This explanation really helped me make sense of it: Monty Hall Problem (best explanation) - Numberphile
It's a good one.
It took me a while to wrap my head around this, but here’s how I finally got it:
There are three doors and one prize, so the odds of the prize being behind any particular door are 1/3. So let’s say you choose door #1. There’s a 1/3 chance that the prize is behind door #1 and, therefore, a 2/3 chance that the prize is behind either door #2 OR door #3.
Now here’s the catch. Monty opens door #2 and reveals that it does not contain the prize. The odds are the same as before – a 1/3 chance that the prize is behind door #1, and a 2/3 chance that the prize is behind either door #2 or door #3 – but now you know definitively that the prize isn’t behind door #2, so you can rule it out. Therefore, there’s a 1/3 chance that the prize is behind door #1, and a 2/3 chance that the prize is behind door #3. So you’ll be twice as likely to win the prize if you switch your choice from door #1 to door #3.
First, fuck you! I couldn't sleep. The possibility to win the car when you change is the possibility of your first choice to be goat, which is 2/3, because you only win when your first choice is goat when you always change.
x1: you win
x2: you change
x3: you pick goat at first choice
P(x1|x2,x3)=1 P(x1)=1/2 P(x3)=2/3 P(x2)=1/2
P(x1|x2) =?
Chain theory of probability:
P(x1,x2,x3)=P(x3|x1,x2)P(x1|x2)P(x2)=P(x1|x2,x3)P(x2|x3)P(x3)
From Bayes theorem: P(x3|x1,x2)= P(x1|x2,x3)P(x2)/P(x1) =1
x2 and x3 are independent P(x2|x3)=P(x2)
P(x1| x2)=P(x3)=2/3 P(x2|x1)=P(x1|x2)P(x2)/P(X1)=P(x1|x2)
P(x1=1|x2=0) = 1- P(x1=1|x2=1) = 1\3 is the probability to win if u do not change.
Why do you have a P(x1) = 1/2 at the start? I'm not sure what x1 means if we don't specify a strategy.
Just count the number of possibilities. If you change there there two possible first choices to win + if you do not change 1 possible choice to win = 3. If you change there is one possible first choice to lose + if you do not change there two possible first choices to lose=3 P(x1)=P(x1') = 3/6
Ah, so it's the probability you win by playing randomly. Gotcha. That makes sense, it becomes a choice between 2 doors
Without condition would be more technically correct term but yes
Goldbach's Conjecture: Every even natural number > 2 is a sum of 2 prime numbers. Eg: 8=5+3, 20=13+7.
https://en.m.wikipedia.org/wiki/Goldbach's_conjecture
Such a simple construct right? Notice the word "conjecture". The above has been verified till 4x10^18 numbers BUT no one has been able to prove it mathematically till date! It's one of the best known unsolved problems in mathematics.
Wtf !
How can you prove something in math when numbers are infinite? That number you gave if it works up to there we can call it proven no? I'm not sure I understand
There are many structures of proof. A simple one might be to prove a statement is true for all cases, by simply examining each case and demonstrating it, but as you point out this won't be useful for proving statements about infinite cases.
Instead you could assume, for the sake of argument, that the statement is false, and show how this leads to a logical inconsistency, which is called proof by contradiction. For example, Georg Cantor used a proof by contradiction to demonstrate that the set of Natural Numbers (1,2,3,4...) are smaller than the set of Real Numbers (which includes the Naturals and all decimal numbers like pi and 69.6969696969...), and so there exist different "sizes" of infinity!
For a method explicitly concerned with proofs about infinite numbers of things, you can try Proof by Mathematical Induction. It's a bit tricky to describe...
Wikipedia says:
Bear in mind, in formal terms a "proof" is simply a list of true statements, that begin with axioms (which are true by default) and rules of inference that show how each line is derived from the line above.
Very cool and fascinating world of mathematics!
Just to add to this. Another way could be to find a specific construction. If you could for example find an algorithm that given any even integer returns two primes that add up to it and you showed this algorithm always works. Then that would be a proof of the Goldbach conjecture.
As you said, we have infinite numbers so the fact that something works till 4x10^18 doesn't prove that it will work for all numbers. It will take only one counterexample to disprove this conjecture, even if it is found at 10^100. Because then we wouldn't be able to say that "all" even numbers > 2 are a sum of 2 prime numbers.
So mathematicians strive for general proofs. You start with something like: Let n be any even number > 2. Now using the known axioms of mathematics, you need to prove that for every n, there always exists two prime numbers p,q such that n=p+q.
Would recommend watching the following short and simple video on the Pythagoras theorem, it'd make it perfectly clear how proofs work in mathematics. You know the theorem right? For any right angled triangle, the square of the hypotenuse is equal to the sum of squares of both the sides. Now we can verify this for billions of different right angled triangles but it wouldn't make it a theorem. It is a theorem because we have proved it mathematically for the general case using other known axioms of mathematics.
https://youtu.be/YompsDlEdtc
The four-color theorem is pretty cool.
You can take any map of anything and color it in using only four colors so that no adjacent “countries” are the same color. Often it can be done with three!
Maybe not the most mind blowing but it’s neat.
Thanks for the comment! It is cool and also pretty aesthetically pleasing!
Your map made me think how interesting US would be if there were 4 major political parties. Maybe no one will win the presidential election 🤔
What about a hypothetical country that is shaped like a donut, and the hole is filled with four small countries? One of the countries must have the color of one of its neighbors, no?
I think the four small countries inside would each only have 2 neighbours. So you could take 2 that are diagonal and make them the same colour.
Looks to be that way one of the examples given on the wiki page. It is still however an interesting theory, if four countries touching at a corner, are the diagonal countries neighbouring each other or not. It honestly feels like a question that will start a war somewhere at sometime, probably already has.
In graph theory there are vertices and edges, two shapes are adjacent if and only if they share an edge, vertices are not relevant to adjacency. As long as all countries subscribe to graph theory we should be safe
The only problem with that it that it requires all countries to agree to something, and that seems to become harder and harder nowadays.
Someone beat me to it, so I thought I'd also include the adjacency graph for the countries, it can be easier to see the solution to colouring them.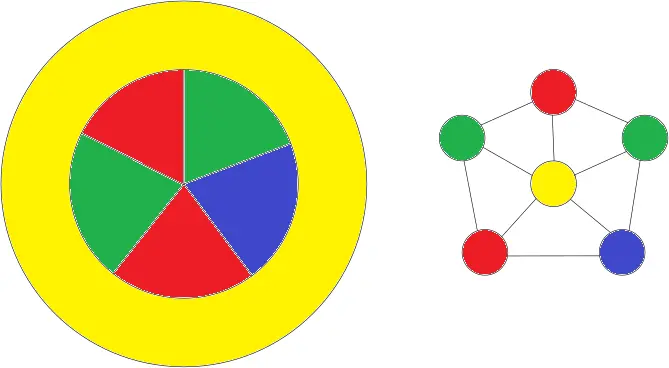
But each small country has three neighbors! Two small ones, and always the big donut country. I attached a picture to my previous comment to make it more clear.
In your example the blue country could be yellow and that leaves the other yellow to be blue. Now no identical colors touch.
You still have two red countries touching each other, what are you talking about?
Oops I meant the red one goes blue.
Whoops I should've been clearer I meant two neighbours within the donut. So the inside ones could be 2 or 3 colours and then the donut is one of the other 2 or the 1 remaining colour.
You're right. Bad example from my side. But imagine this scenario:
That map is actually still quite similar to the earlier example where all 4 donut hole countries are the same. Once again on the right is the adjacency graph for the countries where I've also used a dashed line to show the only difference in adjacency.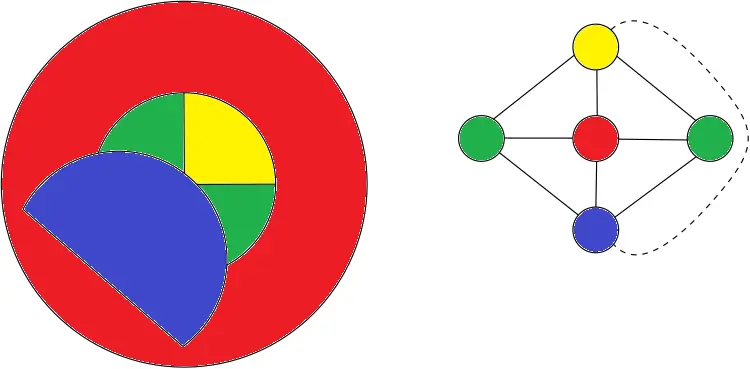
Oh wow, now I feel dumb. Thanks.
Feeling dumb is just the first step in learning something new
Make purple yellow and one of the reds purple.
...There is no purple though?
In that image, you could color yellow into purple since it's not touching purple. Then, you could color the red inner piece to yellow, and have no red in the inner pieces.
There are some rules about the kind of map this applies to. One of them is "no countries inside other countries."
Not true, see @BitSound's comment.
It does have to be topologically planar (may not be the technical term), though. No donut worlds.
The regions need to be contiguous and intersect at a nontrivial boundary curve. This type of map can be identified uniquely with a planar graph by placing a vertex inside each region and drawing an edge from one point to another in each adjacent region through the bounding curve.
I see.
I read an interesting book about that once, will need to see if I can find the name of it.
EDIT - well, that was easier than expected!
Read the author as Robin Williams
Note you'll need the regions to be connected (or allow yourself to color things differently if they are the same 'country' but disconnected). I forget if this causes problems for any world map.
I suspect that the Belgium-Netherlands border defies any mathematical description.
If you had a 3 dimensional map, would you need more colors to achieve the same results?
Edit: it was explained in your link. It looks like for surfaces in 3D space, this can't be generalized.
this whole thread is the shit.
Isn't the proof of this theorem like millions of pages long or something (proof done by a computer ) ? I mean how can you even be sure that it is correct ? There might be some error somewhere.
I came here to find some cool, mind-blowing facts about math and have instead confirmed that I'm not smart enough to have my mind blown. I am familiar with some of the words used by others in this thread, but not enough of them to understand, lol.
Same here! Great post but I'm out! lol
Nonsense! I can blow both your minds without a single proof or mathematical symbol, observe!
There are different sizes of infinity.
Think of integers, or whole numbers; 1, 2, 3, 4, 5 and so on. How many are there? Infinite, you can always add one to your previous number.
Now take odd numbers; 1, 3, 5, 7, and so on. How many are there? Again, infinite because you just add 2 to the previous odd number and get a new odd number.
Both of these are infinite, but the set of numbers containing odd numbers is by definition smaller than the set of numbers containing all integers, because it doesn't have the even numbers.
But they are both still infinite.
Your fact is correct, but the mind-blowing thing about infinite sets is that they go against intuition.
Even if one might think that the number of odd numbers is strictly less than the number of all natural numbers, these two sets are in fact of the same size. With the mapping n |-> 2*n - 1 you can map each natural number to a different odd number and you get every odd number with this (such a function is called a bijection), so the sets are per definition of the same size.
To get really different "infinities", compare the natural numbers to the real numbers. Here you can't create a map which gets you all real numbers, so there are "more of them".
I may be wrong or have misunderstood what you said but the sets of natural numbers and odd numbers have the same size/cardinality. If there exists a bijection between the two sets then they have the same size.
f(x) = 2x + 1 is such a bijection
For the same reason, N, Z and Q have the same cardinality. The fact that each one is included in the next ones doesn't mean their size is different.
Agree. Uncountable infinities are much more mind blowing. It was an interesting journey realising first that everything like time and distance are continuous when learning math the then realising they're not when learning physics.
This is provably false - the two sets are the same size. If you take the set of all integers, and then double each number and subtract one, you get the set of odd numbers. Since you haven't removed or added any elements to the initial set, the two sets have the same size.
The size of this set was named Aleph-zero by Cantor.
There was a response I left in the main comment thread but I'm not sure if you will get the notification. I wanted to post it again so you see it
Response below
Please feel free to ask any questions! Math is a wonderful field full of beauty but unfortunately almost all education systems fail to show this and instead makes it seem like raw robotic calculations instead of creativity.
Math is best learned visually and with context to more abstract terms. 3Blue1Brown is the best resource in my opinion for this!
Here's a mindblowing fact for you along with a video from 3Blue1Brown. Imagine you are sliding a 1,000,000 kg box and slamming it into a 1 kg box on an ice surface with no friction. The 1 kg box hits a wall and bounces back to hit the 1,000,000 kg box again.
The number of bounces that appear is the digits of Pi. Crazy right? Why would pi appear here? If you want to learn more here's a video from the best math teacher in the world.
https://www.youtube.com/watch?v=HEfHFsfGXjs
That's so cool! Thanks for the reply and the link.
Please feel free to ask any questions! Math is a wonderful field full of beauty but unfortunately almost all education systems fail to show this and instead makes it seem like raw robotic calculations instead of creativity.
Math is best learned visually and with context to more abstract terms. 3Blue1Brown is the best resource in my opinion for this!
Here's a mindblowing fact for you along with a video from 3Blue1Brown. Imagine you are sliding a 1,000,000 kg box and slamming it into a 1 kg box on an ice surface with no friction. The 1 kg box hits a wall and bounces back to hit the 1,000,000 kg box again.
The number of bounces that appear is the digits of Pi. Crazy right? Why would pi appear here? If you want to learn more here's a video from the best math teacher in the world.
https://www.youtube.com/watch?v=HEfHFsfGXjs
Thanks! I appreciate the response. I've seen some videos on 3blue1brown and I've really enjoyed them. I think if I were to go back and fill in all the blank spots in my math experience/education I would enjoy math quite a bit.
I don't know why it appears here or why I feel this way, but picturing the box bouncing off the wall and back, losing energy, feels intuitively round to me.
For me, personally, it's the divisible-by-three check. You know, the little shortcut you can do where you add up the individual digits of a number and if the resulting sum is divisible by three, then so is the original number.
That, to me, is black magic fuckery. Much like everything else in this thread I have no idea how it works, but unlike everything else in this thread it's actually a handy trick that I use semifrequently
That one’s actually really easy to prove numerically.
Not going to type out a full proof here, but here’s an example.
Let’s look at a two digit number for simplicity. You can write any two digit number as 10*a+b, where a and b are the first and second digits respectively.
E.g. 72 is 10 * 7 + 2. And 10 is just 9+1, so in this case it becomes 72=(9 * 7)+7+2
We know 9 * 7 is divisible by 3 as it’s just 3 * 3 * 7. Then if the number we add on (7 and 2) also sum to a multiple of 3, then we know the entire number is a multiple of 3.
You can then extend that to larger numbers as 100 is 99+1 and 99 is divisible by 3, and so on.
Waaaait a second.
Does that hold for every base, where the divisor is 1 less than the base?
Specifically hexidecimal - could it be that 5 and 3 have the same "sum digits, get divisibility" property, since 15 (=3*5) is one less than the base number 16?
Like 2D~16~ is16*2+13 = 45, which is divisible by 3 and 5.
Can I make this into a party trick?! "Give me a number in hexidecimal, and I'll tell you if it's divisible by 10."
Am thinking it's 2 steps:
So if 1 and 2 are "yes", it's divisible by 10.
E.g.
Is this actually true? Have I found a new party trick for myself? How would I even know if this is correct?
You're gonna have to go to a lot of parties
All numbers are dividible by 3. Just saying.
The utility of Laplace transforms in regards to differential systems.
In engineering school you learn to analyze passive DC circuits early on using not much more than ohms law and Thevenin's Theoram. This shit can be taught to elementary schoolers.
Then a little while later, you learn how to do non-finear differential equations to help work complex systems, whether it's electrical, mechanical, thermal, hydrolic, etc. This shit is no walk in the park.
Then Laplace transforms/identities come along and let you turn non-linear problems in time-based space, into much simpler problems in frequency-based space. Shit blows your mind.
THEN a mafacka comes along and teaches you that these tools can be used to turn complex differential system problems (electrical, mechanical, thermal, hydrolic, etc) into simple DC circuits you can analyze/solve in frequency-based space, then convert back into time-based space for the answers.
I know this is super applied calculus shit, but I always love that sweet spot where all the high-concept math finally hits the pavement.
And then they tell you that the fundamental equations for thermal, fluid, electrical and mechanical are all basically the same when you are looking at the whole Laplace thing. It's all the same....
ABSOLUTELY. I just recently capped off the Diff Eq, Signals, and Controls courses for my undergrad, and truly by the end you feel like a wizard. It's crazy how much problem-solving/system modeling power there is in such a (relatively) simple, easy to apply, and beautifully elegant mathematical tool.
e^(pi i) = -1
like, what?
3Blue 1Brown actually explains that one in a way that makes it seem less coincidental and black magic. Totally worth a watch
https://www.youtube.com/watch?v=v0YEaeIClKY
If you think of complex numbers in their polar form, everything is much simpler. If you know basic calculus, it can be intuitive.
Instead of z = + iy, write z = (r, t) where r is the distance from the origin and t is the angle from the positive x-axis. Now addition is trickier to write, but multiplication is simple: (a,b) * (c,d) = (ab, b + d). That is, the lengths multiply and the angles add. Multiplication by a number (1, t) simply adds t to the angle. That is, multiplying a point by (1, t) is the same as rotating it counterclockwise about the origin by an angle t.
The function f(t) = (1, t) then parameterizes a circular motion with a constant radial velocity t. The tangential velocity of a circular motion is perpendicular to the current position, and so the derivative of our function is a constant 90 degree multiple of itself. In radians, that means f'(t) = (1, pi/2)f(t). And now we have one of the simplest differential equations whose solution can only be f(t) = k * e^(t* (1, pi/2)) = ke^(it) for some k. Given f(0) = 1, we have k = 1.
All that said, we now know that f(t) = e^(it) is a circular motion passing through f(0) = 1 with a rate of 1 radian per unit time, and e^(i pi) is halfway through a full rotation, which is -1.
If you don't know calculus, then consider the relationship between exponentiation and multiplication. We learn that when you take an interest rate of a fixed annual percent r and compound it n times a year, as you compound more and more frequently (i.e. as n gets larger and larger), the formula turns from multiplication (P(1+r/n)^(nt)) to exponentiation (Pe^(rt)). Thus, exponentiation is like a continuous series of tiny multiplications. Since, geometrically speaking, multiplying by a complex number (z, z^(2), z^(3), ...) causes us to rotate by a fixed amount each time, then complex exponentiation by a continuous real variable (z^t for t in [0,1]) causes us to rotate continuously over time. Now the precise nature of the numbers e and pi here might not be apparent, but that is the intuition behind why I say e^(it) draws a circular motion, and hopefully it's believable that e^(i pi) = -1.
All explanations will tend to have an algebraic component (the exponential and the number e arise from an algebraic relationship in a fundamental geometric equation) and a geometric component (the number pi and its relationship to circles). The previous explanations are somewhat more geometric in nature. Here is a more algebraic one.
The real-valued function e^(x) arises naturally in many contexts. It's natural to wonder if it can be extended to the complex plane, and how. To tackle this, we can fall back on a tool we often use to calculate values of smooth functions, which is the Taylor series. Knowing that the derivative of e^(x) is itself immediately tells us that e^(x) = 1 + x + x^(2)/2! + x^(3)/3! + ..., and now can simply plug in a complex value for x and see what happens (although we don't yet know if the result is even well-defined.)
Let x = iy be a purely imaginary number, where y is a real number. Then substitution gives e^x = e^(iy) = 1 + iy + i^(2)y^(2)/2! + i^(3)y^(3)/3! + ..., and of course since i^(2) = -1, this can be simplified:
e^(iy) = 1 + iy - y^(2)/2! - iy^(3)/3! + y^(4)/4! + iy^(5)/5! - y^(6)/6! + ...
So we're alternating between real/imaginary and positive/negative. Let's factor it into a real and imaginary component: e^(iy) = a + bi, where
a = 1 - y^(2)/2! + y^(4)/4! - y^(6)/6! + ...
b = y - y^(3)/3! + y^(5)/5! - y^(7)/7! + ...
And here's the kicker: from our prolific experience with calculus of the real numbers, we instantly recognize these as the Taylor series a = cos(y) and b = sin(y), and thus conclude that if anything, e^(iy) = a + bi = cos(y) + i sin(y). Finally, we have e^(i pi) = cos(pi) + i sin(pi) = -1.
Damn that's actually pretty simple way to use differential equations to show this.
Edit. The series one is also pretty simple.
Multiply 9 times any number and it always "reduces" back down to 9 (add up the individual numbers in the result)
For example: 9 x 872 = 7848, so you take 7848 and split it into 7 + 8 + 4 + 8 = 27, then do it again 2 + 7 = 9 and we're back to 9
It can be a huge number and it still works:
9 x 987345734 = 8886111606
8+8+8+6+1+1+1+6+0+6 = 45
4+5 = 9
Also here's a cool video about some more mind blowing math facts
I suspect this holds true to any base x numbering where you take the highest valued digit and multiply it by any number. Try it with base 2 (1), 4 (3), 16 (F) or whatever.
11 X 11 = 121
111 X 111 = 12321
1111 X 1111 = 1234321
11111 X 11111 = 123454321
111111 X 1111111 = 12345654321
You could include 1 x 1 = 1
But thats so cool. Maths is crazy.
Amazing in deed!
Just a small typo in the very last factor
1111111.holt shit
The Fourier series. Musicians may not know about it, but everything music related, even harmony, boils down to this.
Fourier transformed everything
Collatz conjecture or sometimes known as the 3x+1 problem.
The question is basically: Does the Collatz sequence eventually reach 1 for all positive integer initial values?
Here's a Veritasium Video about it: https://youtu.be/094y1Z2wpJg
Basically:
You choose any positive integer, then apply 3x+1 to the number if it's odd, and divide by 2 if it's even. The Collatz conjecture says all positive integers eventually becomes a 4 --> 2 --> 1 loop.
So far, no person or machine has found a positive integer that doesn't eventually results in the 4 --> 2 --> 1 loop. But we may never be able to prove the conjecture, since there could be a very large number that has a collatz sequence that doesn't end in the 4-2-1 loop.
maybe this will make more sense when I watch the veritasium video, but I don't have time to do that until the weekend. How is 3x+1 unprovable? won't all odd numbers multiplied by 3 still be odd? and won't adding 1 to an odd number always make it even? and aren't all even numbers by definition divisible by 2? I'm struggling to see how there could be any uncertainty in this
The number 26 reaches as high as 40 before falling back to 4-2-1 loop. The very next number, 27, goes up to 9232 before it stops going higher. For numbers 1 to 10,000 most of them reach a peak of less than 100,000, but somehow, the number 9663 goes up to 27,114,424 before trending downwards. The uncertainty is that what if there is a special number that doesn't just stop at a peak, but goes on forever. I'm not really good at explaining things, so you're gonna have to watch the video.
Just after going through a few examples in my head, the difficulty becomes somewhat more apparent. let's start with 3. This is odd, so 3(3)+1 = 10. 10 is even so we have 10/2=5.
By this point my intuition tells me that we don't have a very obvious pattern that we can use to decide whether the function will output 4, 2, or 1 by recursively applying the function to its own output, other than the fact that every other number that we try appears to result in this pattern. We could possibly reduce the problem to whether we can guess that the function will eventually output a power of 2, but that doesn't sound to me like it makes things much easier.
If I had no idea whether a proof existed, I would guess that it may, but that it is non-trivial. Or at least my college math courses did not prepare me to find one. Since it looks like plenty of professional mathematicians have struggled with it, I have no doubt that if a proof exists it is non-trivial.
The unproven part is that it eventually will reach 1, not that it's not possible to do the computation. Someone may find a number loop that doesn't eventually reach 1.
Quickly a game of chess becomes a never ever played game of chess before.
Related: every time you shuffle a deck of cards you get a sequence that has never happened before. The chance of getting a sequence that has occurred is stupidly small.
Most of the time, but only as long as the shuffle is actually random. A perfect riffle shuffle on a brand new deck will get you the same result every time, and 8 perfect riffles on a row get you back to where you started.
I'm guessing this is more pronounced at lower levels. At high level chess, I often hear commentators comparing the moves to their database of games, and it often takes 20-30 moves before they declare that they have now reached a position which has never been reached in a professional game. The high level players have been grinding openings and their counters and the counters to the counters so deeply that a lot of the initial moves can be pretty common.
Also, high levels means that games are narrowing more towards the "perfect" moves, meaning that repetition from existing games are more likely.
Oh yes I agree totally!
At those (insane) levels "everyone" knows the "best" move after the choice of opening and for a long time.
But for the millions of games played every day, I guess it's a bit less :-)
Euler's identity, which elegantly unites some of the most fundamental constants in a single equation:
e^(iπ)+1=0
This is the one that made me say out loud, "math is fucking weird"
I started trying to read the explanations, and it just got more and more complicated. I minored in math. But the stuff I learned seems trivial by comparison. I have a friend who is about a year away from getting his PhD in math. I don't even understand what he's saying when he talks about math.
Recall the existence and uniqueness theorem(s) for initial value problems. With this, we conclude that e^(kx) is the unique function f such that f'(x) = k f(x) and f(0) = 1. Similarly, any solution to f'' = -k^(2)f has the form f(x) = acos(kx) + bsin(kx). Now consider e^(ix). Differentiating it is the same as multiplying by i, so differentiating twice is the same as multiplying by i^(2) = -1. In other words, e^(ix) is a solution to f'' = -f. Therefore, e^(ix) = a cos(x) + b sin(x) for some a, b. Plugging in x = 0 tells us a = 1. Differentiating both sides and plugging in x = 0 again tells us b = i. So e^(ix) = cos(x) + i sin(x).
We take for granted that the basic rules of calculus work for complex numbers: the chain rule, and the derivative of the exponential function, and the existence/uniqueness theorem, and so on. But these are all proved in much the same way as for real numbers, there's nothing special behind the scenes.
Time for a deep dive. Wish me luck, lads.
Let us know what you find in the depths.
The one I bumped into recently: the Coastline Paradox
"The coastline paradox is the counterintuitive observation that the coastline of a landmass does not have a well-defined length. This results from the fractal curve–like properties of coastlines; i.e., the fact that a coastline typically has a fractal dimension."
This is my silly contribution: 70% of 30 is equal to 30% of 70. This applies to other numbers and can be really helpful when doing percentages in your head. 15% of 77 is equal to 77% of 15.
I’ve seen this one used in the news when they want to make one side of a statistic stand out.
A/100×B=A×B/100
Seeing mathematics visually.
I am a huge fan of 3blue1brown and his videos are just amazing. My favorite is linear algebra. It was like an out of body experience. All of a sudden the world made so much more sense.
His video about understanding multiple dimensions was what finally made it click for me
Imagine a soccer ball. The most traditional design consists of white hexagons and black pentagons. If you count them, you will find that there are 12 pentagons and 20 hexagons.
Now imagine you tried to cover the entire Earth in the same way, using similar size hexagons and pentagons (hopefully the rules are intuitive). How many pentagons would be there? Intuitively, you would think that the number of both shapes would be similar, just like on the soccer ball. So, there would be a lot of hexagons and a lot of pentagons. But actually, along with many hexagons, you would still have exactly 12 pentagons, not one less, not one more. This comes from the Euler's formula, and there is a nice sketch of the proof here: .
You're missing your link, homie!
It seems that I can't see the link from 0.18.3 instances somehow. Maybe one of these will work: https://math.stackexchange.com/a/18347 https://math.stackexchange.com/a/18347
https://math.stackexchange.com/a/18347The square of any prime number >3 is one greater than an exact multiple of 24.
For example, 7² = 49= (2 * 24) + 1
Does this really hold for higher values? It seems like a pretty good way of searching for primes esp when combined with other approaches.
Every prime larger than 3 is either of form 6k+1, or 6k+5; the other four possibilities are either divisible by 2 or by 3 (or by both). Now (6k+1)² − 1 = 6k(6k+2) = 12k(3k+1) and at least one of k and 3k+1 must be even. Also (6k+5)² − 1 = (6k+4)(6k+6) = 12(3k+2)(k+1) and at least one of 3k+2 and k+1 must be even.
I've read books about prime numbers and I did not know this.
I don't get it,
5² = 25 != (2 * 24) + 111² = 121 != (2 * 24) + 1Could you please help me understand, thanks!
5² = 25 = (1 * 24) + 111² = 121 = (5 * 24) + 1The key thing is that
p² = 24n + 1(forpgreater than 3).Not 2 * 24, but x * 24.
So 5^2 = 1 * 24 +1
11^2 = 5 * 24 + 1
e^(I*pi) = -1
My favorite form, just slightly different,
Euler's identity directly relates all the really cool mathematical constants into one elegant formula:
e,i,π,1, and0I think that is the cooler form but I first saw Euler's ID as =-1
Borsuk-Ulam is a great one! In essense it says that flattening a sphere into a disk will always make two antipodal points meet. This holds in arbitrary dimensions and leads to statements such as "there are two points along the equator on opposite sides of the earth with the same temperature". Similarly one knows that there are two points on the opposite sides (antipodal) of the earth that both have the same temperature and pressure.
Also honorable mentions to the hairy ball theorem for giving us the much needed information that there is always a point on the earth where the wind is not blowing.
Seeing I was a bit heavy on the meteorological applications, as a corollary of Borsuk-Ulam there is also the ham sandwich theorem for the aspiring hobby chefs.
Godel's incompleteness theorem is actually even more subtle and mind-blowing than how you describe it. It states that in any mathematical system, there are truths in that system that cannot be proven using just the mathematical rules of that system. It requires adding additional rules to that system to prove those truths. And when you do that, there are new things that are true that cannot be proven using the expanded rules of that mathematical system.
"It's true, we just can't prove it'.
Incompleteness doesn't come as a huge surprise when your learn math in an axiomatic way rather than computationally. For me the treacherous part is actually knowing whether something is unprovable because of incompleteness or because no one has found a proof yet.
Thanks for the further detail!
That e^pi-pi = 20
As an engineer, i dont know how to feel about this. On the one hand, 19.99999 = 20. But on the other hand, 3^3 - 3 = 24.
you need a space before the second pi
Oh fuck you. I'm going to insert this in place of 20 in some formula and see people have breakdowns.
This is a common one, but the cardinality of infinite sets. Some infinities are larger than others.
The natural numbers are countably infinite, and any set that has a one-to-one mapping to the natural numbers is also countably infinite. So that means the set of all even natural numbers is the same size as the natural numbers, because we can map 0 > 0, 1 > 2, 2 > 4, 3 > 6, etc.
But that suggests we can also map a set that seems larger than the natural numbers to the natural numbers, such as the integers: 0 → 0, 1 → 1, 2 → –1, 3 → 2, 4 → –2, etc. In fact, we can even map pairs of integers to natural numbers, and because rational numbers can be represented in terms of pairs of numbers, their cardinality is that of the natural numbers. Even though the cardinality of the rationals is identical to that of the integers, the rationals are still dense, which means that between any two rational numbers we can find another one. The integers do not have this property.
But if we try to do this with real numbers, even a limited subset such as the real numbers between 0 and 1, it is impossible to perform this mapping. If you attempted to enumerate all of the real numbers between 0 and 1 as infinitely long decimals, you could always construct a number that was not present in the original enumeration by going through each element in order and appending a digit that did not match a decimal digit in the referenced element. This is Cantor's diagonal argument, which implies that the cardinality of the real numbers is strictly greater than that of the rationals.
The best part of this is that it is possible to construct a set that has the same cardinality as the real numbers but is not dense, such as the Cantor set.
Well that's not as hard as it sounds, [0,1] isn't dense in the reals either. It is however dense with respect to itself, in the sense that the closure of [0,1] in the reals is [0,1]. The Cantor set has the special property of being nowhere dense, which is to say that it contains no intervals (taking for granted that it is closed). It's like a bunch of disjointed, sparse dots that has no length or substance, yet there are uncountably many points.
That you can have 5 apples, divide them zero times, and somehow end up with math shitting itself inside-out at you even though the apples are still just sitting there.
You try having 5 apples and divide them into 0 equal groups and you'll shit yourself too.
Except that by dividing the total number zero times means you're not dividing them at all, and therefore by doing nothing you are still left with 5 apples.
Not dividing at all is dividing by 1.
A simple one: Let's say you want to sum the numbers from 1 to 100. You could make the sum normally (1+2+3...) or you can rearrange the numbers in pairs: 1+100, 2+99, 3+98.... until 50+51 (50 pairs). So you will have 50 pairs and all of them sum 101 -> 101*50= 5050. There's a story who says that this method was discovered by Gauss when he was still a child in elementary school and their teacher asked their students to sum the numbers.
Euler's identity is pretty amazing:
e^iπ + 1 = 0
To quote the Wikipedia page:
The fact that an equation like that exists at the heart of maths - feels almost like it was left there deliberately.
Fermat's Last Theorem
x^n + y^n = z^n has no solutions where n > 2 and x, y and z are all natural numbers. It's hard to believe that, knowing that it has an infinite number of solutions where n = 2.
Pierre de Format, after whom this theorem was named, famously claimed to have had a proof by leaving the following remark in some book that he owned: "I have a proof of this theorem, but there is not enough space in this margin". It took mathematicians several hundred years to actually find the proof.
I find the logistic map to be fascinating. The logistic map is a simple mathematical equation that surprisingly appears everywhere in nature and social systems. It is a great representation of how complex behavior can emerge from a straightforward rule. Imagine a population of creatures with limited resources that reproduce and compete for those resources. The logistic map describes how the population size changes over time as a function of its current size, and it reveals fascinating patterns. When the population is small, it grows rapidly due to ample resources. However, as it approaches a critical point, the growth slows, and competition intensifies, leading to an eventual stable population. This concept echoes in various real-world scenarios, from describing the spread of epidemics to predicting traffic jams and even modeling economic behaviors. It's used by computers to generate random numbers, because a computer can't actually generate truly random numbers. Veritasium did a good video on it: https://www.youtube.com/watch?v=ovJcsL7vyrk
I find it fascinating how it permeates nature in so many places. It's a universal constant, but one we can't easily observe.
Here's a fun one - you know the concept of regular polyhedra/platonic solids right? 3d shapes where every edge, angle, and face is the same? How many of them are there?
Did you guess 48?
There's way more regular solids out there than the bog standard set of DnD dice! Some of them are easy to understand, like the Kepler-poisont solids which basically use a pentagramme in various orientations for the face shape (hey the rules don't say the edges can't intersect!) To uh...This thing. And more! This video is a fun breakdown (both mathematically and mentally) of all of them.
Unfortunately they only add like 4 new potential dice to your collection and all of them are very painful.
I believe this is the primary distinction
I heard that Pythagoras killed a man on a fishing trip because he solved a problem first.
That's a pretty wild math tale!
When all you learn about Pythagoras is that he was a mathematician known for triangles then learning about the cult and the murder definitely takes you by surprise
The Banach - Tarski Theorm is up there. Basically, a solid ball can be broken down into infinitely many points and rotated in such a way that that a copy of the original ball is produced. Duplication is mathematically sound! But physically impossible.
https://en.m.wikipedia.org/wiki/Banach%E2%80%93Tarski_paradox
Only if you accept the axiom of choice :P
How Gauss was able to solve 1+2+3...+99+100 in the span of minutes. It really shows you can solve math problems by thinking in different ways and approaches.
50*101?
Yep. N * (n + 1) / 2.
You can think of it as.
Not so much a fact, but I've always liked the prime spirals: https://en.wikipedia.org/wiki/Ulam_spiral
Also, not as impressive as the busy beaver, but Knuth's up-arrow notation is cool: https://en.wikipedia.org/wiki/Knuth%27s_up-arrow_notation
Knuth's arrow shows up in... Magic the Gathering. There's a challenge of "how much damage can you deal with just 3 cards and without infinitely repeating loops?". Turns out that stacking doubler effects can get us really high. https://www.polygon.com/23589224/magic-phyrexia-all-will-be-one-best-combo-attacks-tokens-vindicator-mondrak
Thanks for sharing! (No worries, changed the title from "fact" to "thing" to be a bit more broad)
To me, personally, it has to be bezier curves. They're not one of those things that only real mathematicians can understand, and that's exactly why I'm fascinated by them. You don't need to understand the equations happening to make use of them, since they make a lot of sense visually. The cherry on top is their real world usefulness in computer graphics.
Non-Euclidean geometry.
A triangle with three right angles (spherical).
A triangle whose sides are all infinite, whose angles are zero, and whose area is finite (hyperbolic).
I discovered this world 16 years ago - I'm still exploring the rabbit hole.
Spherical geometry isn't even that weird because we experience it on earth at large scales.
I'm not sure Earth would be a correct analogy for spherical geometry. Correct me if I'm wrong, but spherical geometry is when the actual space curvature is a sphere, which is different from just living on a sphere.
CodeParade made a spherical/hyperbolic geometry game, and here's one of his devlogs explaining spherical curvature: https://www.youtube.com/watch?v=yY9GAyJtuJ0
A sphere is a perfect model of spherical geometry. It's just a 2-dimensional one, the spherical equivalent of a plane we might stand on as opposed to the space we live in. A sphere is locally flat (locally Euclidean/plane-like) but intrinsically curved, and indeed can have triangles with 3 right angles (with endpoints on a pole and the equator.)
Ah, gotcha! Spherical and hyberbolic geometries always mess with my mind a bit. Thanks for the explanation!
Oh yeah I'm subscribed to codeparade! I know it's not a perfect analogue but since it's such a large scale, our perspective makes it look flat. So at long distances it feels like you're moving in a straight line when you're really not.
The Julia and Mandelbrot sets always get me. That such a complex structure could arise from such simple rules. Here's a brilliant explanation I found years back: https://www.karlsims.com/julia.html
Great thread. I'm just reading and watching stuff this afternoon now
Glad you are enjoying it! Please feel free to share any other channels like Computerphile, Numberphile, Mutual Information, & Veritasium. It's difficult to find gems nowadays on YT.
I like Stand-up Maths, usually starts with a real-life situation and escalates into proper math, sometimes also programming shows up.
Well, if you ever want to find some more mathtubers, just browse the #SoMe2 or #SoMe3 hashtags on YouTube. It led me to Morphocular, who does great videos with great visual quality similar to 3B1B. Another great channel is Another Roof with a completely different approach of videomaking. VSauce also has some good videos on math topics, if you like him.
As mentioned by @Blyfh, 3Blue 1Brown is great.
I also came across this channel by Freya Holmér recently that does more Long Lecture videos on math for video game programmers. I found the the one on splines to be quite enlightening (as I had recently been doing a lot of spline stuff and struggling with third party packages).
https://www.youtube.com/@Acegikmo
Late to the party but one channel I came across was Combo Class, who should get more love! I adore his setup and his passion for weird maths stuff.
Absolutely strange in the most endearing way.
Maybe a bit advanced for this crowd, but there is a correspondence between logic and type theory (like in programming languages). Roughly we have
Proposition ≈ Type
Proof of a prop ≈ member of a Type
Implication ≈ function type
and ≈ Cartesian product
or ≈ disjoint union
true ≈ type with one element
false ≈ empty type
Once you understand it, its actually really simple and "obvious", but the fact that this exists is really really surprising imo.
https://en.m.wikipedia.org/wiki/Curry%E2%80%93Howard_correspondence
You can also add topology into the mix:
https://en.m.wikipedia.org/wiki/Homotopy_type_theory
One could say that Homotopy type theory is really HoTT right now (pun intended.) I've never actually used it in connection with topology though.
Also, overall higher order logics are really cool if you're a programmer and love the abstract :)
There are more infinite real numbers between 0 and 1 than whole numbers.
https://en.wikipedia.org/wiki/Countable_set
The 196,883-dimensional monster number (808,017,424,794,512,875,886,459,904,961,710,757,005,754,368,000,000,000 ≈ 8×10^53) is fascinating and mind-boggling. It's about symmetry groups.
There is a good YouTube video explaining it here: https://www.youtube.com/watch?v=mH0oCDa74tE
As someone who took maths in university for two years, this has successfully given me PTSD, well done Lemmy.
The fact that complex numbers allow you to get a much more accurate approximation of the derivative than classical finite difference at almost no extra cost under suitable conditions while also suffering way less from roundoff errors when implemented in finite precision:
(x and epsilon are real numbers and f is assumed to be an analytic extension of some real function)
Higher-order derivatives can also be obtained using hypercomplex numbers.
Another related and similarly beautiful result is Cauchy's integral formula which allows you to compute derivatives via integration.
This is the first one that's new to me! Really interesting, I guess the big problem is that you need to actually be able to evaluate the analytic extension.
Well, that's something I hadn't seen before.
What?
The formula you linked is wrong, it should be O(epsilon). It's the same as for real numbers, f(x+h) = f(x) + hf'(x) + O(h^(2)). If we assume f(x) is real for real x, then taking imaginary parts, im(f(x+ih)) = 0 + im(ihf'(x)) + O(h^(2)) = hf'(x)) + O(h^(2)).
I can assure you that you're the one who's wrong, the order 2 term is a real number which means that it goes away when you take the imaginary part, leaving you with a O(epsilon^3) which then becomes a O(epsilon^2) after dividing by epsilon. This is called complex-step differentiation.
Oh, okay.
The Monty hall problem makes me irrationally angry.
I found the easiest way to think about it as if there are 10 doors, you choose 1, then 8 other doors are opened. Do you stay with your first choice, or the other remaining door? Or scale up to 100. Then you really see the advantage of swapping doors. You have a higher probability when choosing the last remaining door than of having correctly choosen the correct door the first time.
Edit: More generically, it's set theory, where the initial set of doors is 1 and (n-1). In the end you are shown n-2 doors out of the second set, but the probability of having selected the correct door initially is 1/n. You can think of it as switching your choice to all of the initial (n-1) doors for a probability of (n-1)/n.
Holy shit this finally got it to click in my head.
I find the easiest way to understand Monty Hall is to think of it in a meta way:
Situation A - A person picks one of three doors, 1 n 3 chance of success.
Situation B - A person picks one of two doors, 1 in 2 chance of success.
If you were an observer of these two situations (not the person choosing doors) and you were gonna bet on which situation will more often succeed, clearly the second choice.
But the issue is that by switching doors, you have a 66% chance of winning, it doesn't drop to 50% just because there are 2 doors, it's still 33% on the first door, 66% on the other doors (as a whole), for which we know one is not correct and won't choose.
is the key words here
individually the door has that 1:2 chance, but the scenario has more context and information and thus better odds. Choosing scenario B over scenario A is a better wager
you aren't talking about the Monty Hall problem then
Only to somebody who didn't know about the choice being made!
I don't understand how this relates to the problem. Yes 50 percent is greater than 33 percent, but that's not what the Monty hall problem is about. The point of the exercise is to show that when the game show host knowingly (and it is important to state that the host knows where the prize is) opens a door, he is giving the contestant 33 percent extra odds.
Incompleteness is great.. internal consistency is incompatible with universality.. goes hand in hand with Relativity.. they both are trying to lift us toward higher dimensional understanding..
Integrals. I can have an area function, integrate it, and then have a volume.
And if you look at it from the Rieman sum angle, you are pretty much adding up an infinite amount of tiny volumes (the area * width of slice) to get the full volume.
Geometric interpretation of integration is really fun, it's the analytic interpretation that most people (and I) find harder to understand.
If you work in numerically solving integrals using computers, you realise that it's all just adding tiny areas.
I finally understand what divergent integrals are intuitively when I encountered one while trying to do a calculation on a computer.
One thing that definitely feels like "magic" is Monstrous Moonshine (https://en.wikipedia.org/wiki/Monstrous_moonshine) and stuff related to the j-invariant e.g. the fact that exp(pi*sqrt(163)) is so close to an integer (https://en.wikipedia.org/wiki/Heegner_number#Almost_integers_and_Ramanujan.27s_constant). I hardly understand it at all but it seems mind-blowing to me, almost in a suspicious way.
Saving this thread! I love math, even if I'm not great at it.
Something I learned recently is that there are as many real numbers between 0 and 1 as there are between 0 and 2, because you can always match a number from between 0 and 1 with a number between 0 and 2. Someone please correct me if I mixed this up somehow.
You are correct. This notion of “size” of sets is called “cardinality”. For two sets to have the same “size” is to have the same cardinality.
The set of natural numbers (whole, counting numbers, starting from either 0 or 1, depending on which field you’re in) and the integers have the same cardinality. They also have the same cardinality as the rational numbers, numbers that can be written as a fraction of integers. However, none of these have the same cardinality as the reals, and the way to prove that is through Cantor’s well-known Diagonal Argument.
Another interesting thing that makes integers and rationals different, despite them having the same cardinality, is that the rationals are “dense” in the reals. What “rationals are dense in the reals” means is that if you take any two real numbers, you can always find a rational number between them. This is, however, not true for integers. Pretty fascinating, since this shows that the intuitive notion of “relative size” actually captures the idea of, in this case, distance, aka a metric. Cardinality is thus defined to remove that notion.
Fantastic explanation. Thank you!
Edit: I guess I should have said rational numbers vs real. I just looked up the difference.
Szemeredis regularity lemma is really cool. Basically if you desire a certain structure in your graph, you just have to make it really really (really) big and then you're sure to find it. Or in other words you can find a really regular graph up to any positive error percentage as long as you make it really really (really really) big.
An arithmetic miracle:
Let's define a sequence. We will start with 1 and 1.
To get the next number, square the last, add 1, and divide by the second to last. a(n+1) = ( a(n)^2 +1 )/ a(n-1) So the fourth number is (2*2+1)/1 =5, while the next is (25+1)/2 = 13. The sequence is thus:
1, 1, 2, 5, 13, 34, ...
If you keep computing (the numbers get large) you'll see that every time we get an integer. But every step involves a division! Usually dividing things gives fractions.
This last is called the somos sequence, and it shows up in fairly deep algebra.
The infinite sum of all the natural numbers 1+2+3+... is a divergent series. But it can also be shown to be equivalent to -1/12. This result is actually used in quantum field theory.
I don't suppose you know the exact application in QFT? I assume it's used for some renormalization scheme?
Small nit: you don't compute sigma, you prove a value for a given input. Sigma here is uncomputable.
was not aware of the machines halting only iff conjectUres are true, tho. Thats a flat out amazing construction.
This one isn't terribly mind-blowing, though it does have some really cool uses. I always remember it because of its name: Witch of Agnesi
The birthday paradox
Told ya. That's why i don't like math: the syntax is awkward.
I love this thread! It shall be saved.